신경망 with [개발자를 위한 머신러닝] (1/2)

신경망

일반적인 분류, 군집의 블로그 설명은 넘어가기로 한다

l 신경망 모델 역사
l 신경망과 해결 가능한 문제
l 다층 퍼셉트론
l 이진 함수 모델링을 위한 간단한 신경 계층 구현

1. 신경망 모델 역사

맥클러치와 피츠 모델

1940년대 중반 인간 두뇌의 학습 기능을 표현하는 최초의 수학적 방법은 Warren McCulloch 와 Walter Pitts 가 1943년 발표한 [A Logical calculus of ideas immanent in nervous activity]에 맥클러치와 피츠 모델이다

맥클러치와 피츠 모델

모델에서 조정할 파라미터를 나타내기 위해 일반적으로 w 문자를 사용한다.

퍼셉트론 모델

인공 뉴런을 구현하는 가장 간단한 방법중 하나

1. 임의 분포로 가중치를 초기화
2. 입력 벡터를 선택하고 네트워크에 사용
3. 지정한 입력 벡터와 가중치 값에 대한 네트워크의 출력 y'를 계산
4. y' != y 일때 error 를 추가해 모든 가중치(w)를 수정
5. 2단계로 돌아감 y'=y일때까지 반복

퍼셉트론 모델

퍼셉트론(Perceptron) 은 맥클러치와 피츠 모델을 바탕으로 만들어 졌지만, 오차 계산하는 학습 메커니즘이 추가 됐다는 점이다
퍼셉트론 모델 에 대해 자세히 설명한 블로그이다

예측 값 개선: ADALINE(Adaptive Linear Neuron) 알고리즘

퍼셉트론 모델에 비해 한층 진화된 알고리즘
오차 계산할때 그랜디언트 디센트 방식을 사용하고 활성화 출력이 가중치의 합계에 적용되기 전에 오차가 측정된 지점을 변경하는 과정이 추가됨

1. 임의 분포로 가중치를 초기화
2. 입력 벡터를 선택하고 네트워크에 사용
3. 지정한 입력 벡터와 가중치 값에 대한 네트워크의 출력 y'를 계산
4. 사용할 출력 값을 합계 후의 출력 값
5. 모델 출력을 올바른 레이블 O 와 비교해 오차를 계산
6. if y' != y, 반복적인 그래디언트 디센트를 사용해 가중치를 조정
7. 2단계로 돌아가 y'가 수렴할때 까지 반복

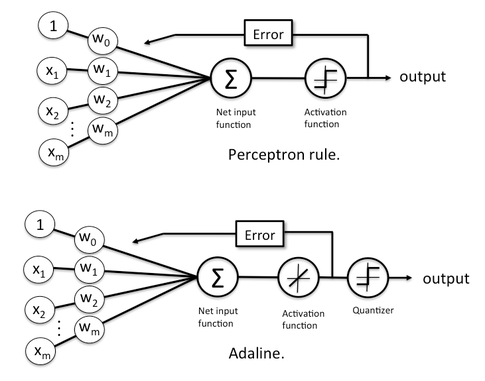퍼셉트론 모델과 ADALINE 알고리즘 비교

퍼셉트론과 ADALINE 알고리즘

• 유사점
• 단층 신경 모델
• 이진 분류를 위한 분류 모델
• 선형 결정 경계를 가짐
• 임계 함수를 사용
• 차이점
• 퍼셉트론은 가중치를 훈련하기 위해 최종 분류 결정 값을 사용
• ADALINE은 연속적인 예측 값을 사용해 모델 계수를 학습 하고 연속적인 부동소수점 값으로 오차의 미묘한 변화를 측정

하지만 두 모델은 초기 모델로 많은 제약사항이 있다.
1969년에 출판된 Minsky 와  Papert 에 의한 'Perceptrons' 란 저서에서 단층 퍼셉트론은 선형 분리의 단순한 예인 XOR 문제도 해결할 수 없다는 사실을 입증 했다.
추후 1970년대 중반 역전파(Back-propagation) 모델이 나오게 되면서 다층 퍼셉트론 모델의 기반이 됨

참고

https://www.packtpub.com/big-data-and-business-intelligence/machine-learning-developers

http://www.aistudy.co.kr/neural/McCulloch_Pitts.htm
http://www.aistudy.com/neural/perceptron.htm
http://www.aistudy.com/neural/backpropagation.htm
https://sacko.tistory.com/10
https://kr.deductiontheory.com/2017/05/blog-post.html
https://sebastianraschka.com/faq/docs/diff-perceptron-adaline-neuralnet.html